On the
first day of my VU Algorithms course Dr. Spinrad asked the class to
describe the difference between an algorithm and an equation. In a class of
forty students, I was surprised how many people stuttered and second-guessed
their framework for describing the difference. Most all of the students had
taken CS101 and CS201 previously. They have worked with computer algorithms
such as those for searching and sorting and have almost all taken four
semesters of calculus. What caused this lack of confidence?
Based on
the reading this week, I think this can be addressed through the stronger
implementation of computational thinking ideas into mathematics curriculums and
is emphasized by “reciprocal relationship” notion discussed by Weintrop for
“using computation to enrich mathematics and science learning and using
mathematics and science contexts to enrich computational learning” – a concept
that seems to correlate to the interdisciplinary nature of computational
thinking addressed by Wing that computational thinking is for everyone.
However,
how this reciprocal relationship is implemented in the classroom seems to be
different between the two papers. I felt that Weintrop over-emphasized the role
of computing tools as what constitutes computational thinking. For instance, in
terms of data – collecting, creating, manipulating, analyzing and visualizing
data are included as computational thinking in math and science. Based on my
understanding of Wing’s computational thinking description, data is involved when
a significant large amount of data is needed or used to solve complex
functions: it is how the data is used, not the collection of the data. Weintrop
also seemed to emphasize the role of programming in the problem solving aspect
of computational thinking (a concept that Wing may disagree with as she noted
that you can teach computational thinking skills without programming).
Overall,
when combining these papers with my previous understanding of computational
thinking curriculums based on the papers we have read as a class, I’ve created
what I see as an example timeline of applying computational thinking to a
mathematical concept as a means of potentially interesting students in becoming
programmers:
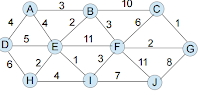
Layer One: Middle School -- students are given this
map and are asked to find a way to connect all nodes/letters. I believe most
students will be in or have taken Algebra and the most common method of solving
the problem may be to find every possible combination, add each combination up
and select the combination with the smallest value at the end.
Layer Two: Algebra 1/Geometry, High School – add a
time constraint and introduce the notion of an algorithm. Students need to find
the shortest path possible given the time constraint. The concept will be that
it may not be the most efficient in the end, but they need to think of the
requirements, come up with a plan (algorithm) and solve. My guess is that
students will see 10 nodes so they will need a minimum of 9 edges. They can
circle the 9 smallest values for edges and see if there is any way all nodes
can be connected using those edges.
Layer Three: Pre-Calc, High School – introduce the
concept of searching. Students can start with any node (because they all have
to be connected) and see if they can find the shortest path going step by step.
Layer Four: Calc/AP Computer Science – for those
students that enjoyed the problem solving/algorithmic process, show how Google’s
algorithms make it possible to find the shortest directions for users on Google
Maps. Programming not introduced until this stage.
I appreciate your example being divided into layers, I think this provides clarity to the question of how computational thinking could be introduced and then continued as students' growth and development evolves. I also like how you build off their previous knowledge as well as integrate computational thinking within the context of their curriculum.
ReplyDeleteHello Nicole,
ReplyDeleteThank you for your thought provoking posts! I always enjoy reading them :)
In terms of the difference between an equation and algorithm, I think the latter is more of an automated approach to resolve problems. Algorithms capture "patterns" among equations and, I believe, are supposed to automate problem solving through these patterns.
I think you make a wonderful point by differentiating between data collection and computational thinking. While I approve that the two concepts are essentially separate, I nevertheless believe that what Weintrop et al. were actually pointing to is the fact that there is a practice of collecting data via computational tools, and this practice requires particular computational skills, such as "the design of a collection protocol, recording and storage." (p.136). As a matter of fact, Wing considers computational thinking as "the thought processes involved in formulating problems and their solutions so that the solutions are represented in forms that can be effectively carried out by an information processing agent." Accordingly, data collection could require particular computational thinking skills that are specific to the field of data collection. For example, what are the best approaches to collect and record big data?
Finally, I cannot actually separate between programming and computational skills. It is like separating between ideas and the language. The languages that we use to express our ideas shape the ideas that we construct. In a very similar sense, different programming languages shape computational thinking by affording and constraining the expression of particular ideas and algorithms. Knowing what is possible and not possible in the languages that we utilize is essential in shaping the solutions we construct for our problems.
Would love to hear your thoughts on these ideas!
Thank you for your comment, Carol. In order to better address your ideas, I believe I will need additional information on how you are countering the thoughts I discuss. For instance, I agree with you that there are certain computational thinking skills needed for data processing, but in terms of learning how to use a computational tool (say, Excel to record data) - I do not believe that is necessarily a computational thinking skill. Now, when you are creating a database or use a programming language to develop data structures (as they do a small amount in CS1101 and more-so in CS 2201 - both college level courses) - then you are using computational thinking skills in terms of data collection and processing. In fact, I also reference Wing's inclusion of the data analysis process in the blog. Unfortunately, I think there is a lot of computational thinking growth and development needed in lower, middle, and upper school before students are truly able to utilize data management and analysis to enhance computational thinking.
DeleteHowever, with that being said: the spanning tree idea I discuss involves data collection and analysis without programming until certain skills have been acquired. Even in middle school, I assumed that students would find every possible path, add up the costs, and store that data somewhere to compare later on. That process I believe is computational thinking. The actual use of a "computational tool" to store the data (likely Excel/Sheets at that level) - I do not see that usage as computational thinking.
Finally, in terms of programming and computational thinking. I am not separating the two and do not believe Wing does either. For me, programming is another tool to better help develop computational thinking skills, but I do not think it is required to develop certain computational thinking skills (example: the spanning tree). In addition, for your comment "affording and constraining the expression of particular ideas and algorithms" -- I see computational thinking as the development of those algorithms, the problem solving process, and the use of a programming language as simply a tool to implement your algorithm. Programming languages are changing and as I mentioned last week (although it will be quite some time before this is reality) - programming languages may not be needed, but the process of developing algorithms to complete a task will be.